DMN and SBVR can be used to specify the same kind of business logic. This post compares the two, looking at strenghths and weaknesses of each. It was inspired by Nick Broom’s excellent Nov 2014 comparison of DMN (OMG’s Decision Model and Notation) and TDM (Sapiens’ The Decision Model):
https://horizonbusinessarchitecture.com/2020/04/24/next-stop-dmntdm-interchange/
I’m using exactly the same example case, summarised by Nick as “A student can enrol for a course if the maximum number of students has not yet been exceeded and [the student] is not already taking more than 4 courses” (the “Enrollment Example”).
First, I present this example in DMN. Then, I present the same example in SBVR. Last, I discuss how the two compare. My conclusions are:
- DMN models event-based procedure calls, SBVR is bidirectional
- DMN is easier to implement
- DMN is currently stronger at providing overview and completeness
- SBVR is easier for domain experts to validate
- SBVR has more natural business language
What this Post is Not
Before launching into the example case, let’s side-step for a moment and consider what this post is not.
First, it’s not a tutorial. You already need to be aware of what DMN, BPMN and SBVR (the OMG specifications) are. But I’ll do my best to keep you on board, even if you don’t have detailed knowledge of these standards.
Second, it’s not a scientific article. I am well aware that theoretic discussion is possible at many levels. For example, is the example a case of “business logic”, “implementation specs”, or a combination of both? Do SBVR and DMN not have different intended uses? If we want to compare SBVR properly to DMN, do we not need to address its Logical Formalisation clauses, instead of just its conceptual metamodel? and so on.
These are all legitimate concerns, but they distract from the point I’m trying to make in this post. Both DMN and SBVR do offer formalisations of the kind of logic that is summarily expressed by “A student can enrol for a course if the maximum number of students has not yet been exceeded and the student is not already taking more than 4 courses”. My only ambition here is to discuss interesting differences between those two formalisations.
The Enrollment Example in DMN
This section is an imitation of OMG’s own examples provided in Clause 11 of the DMN 1.0 specification, but this time applied to the Enrollment Example.
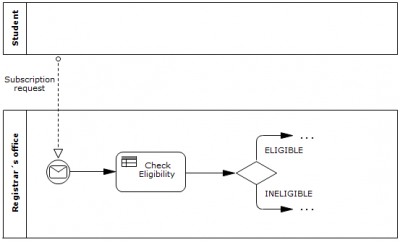
Fig. 1 shows a BPMN process fragment that contains a call for a decision. It starts with a student requesting to be enrolled for a course. A decision must be made as to whether that student is eligible to be enrolled for that course. The icon inside the Check Eligibility activity symbol shows that the activity is a Business Rule Task, meaning that such Business Rules as may be expressed in DMN or SBVR are needed to carry the process further:
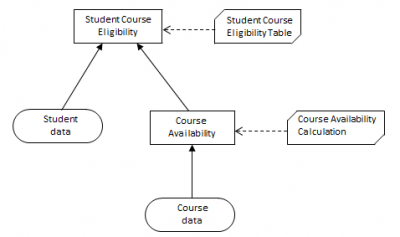
The top-level decision on whether the student is eligible for enrollment on the course requires student data, course data, and logic laid down in a calculation instruction and in a decision table. Fig. 2, a DRD (Decision Requirement Diagram), provides an overview of these requirements and how they hang together. DRD is a diagram type on which DMN 1.0 is normative:
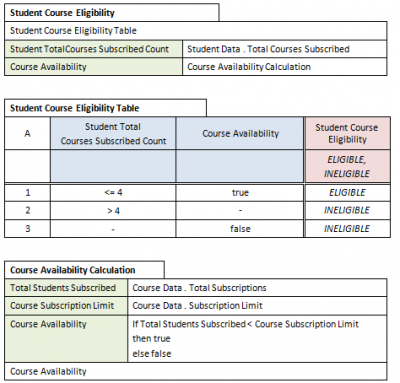
Details of the various elements in the DRD are given in the so-called “boxed expressions” of Fig. 3. While DMN 1.0 is normative on most aspects of boxed expressions, Fig. 3 is only one of several possible ways of arranging the example material. Some cells have green, blue or red background colour, but DMN is not normative on colour:
The Enrollment Example in SBVR
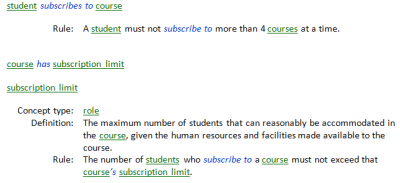
The SBVR specification is not normative on any aspect to do with presentation format. However, its own specification text demonstrates a possible format, and I used this format as a model for drawing up Fig. 4. Like DMN, SBVR does not legislate on colour, but the use of green colour for noun concepts and blue colour for verb concepts is widely seen as a hallmark of SBVR:
(Fig. 4 is as short as it is for a good reason. Subscription limit is a role in a so-called binary verb concept, which could be termed ‘course caters for number of students’ and could be formally defined, as well as being shown to involve ranging over the cardinality of a set of students, but none of these modelling details contributes anything to the points I want to make.)
Unlike DMN, SBVR is not normative on diagramming. A simple class diagram is, however, often included to visualise concept structure. Such a diagram shows key noun concepts (here, student, course and subscription limit) and the relationships between them (Fig. 5):
Comparing DMN to SBVR
Even this small example shows up noteworthy differences between DMN and SBVR. I hope that the informal observations in the next sections will help you decide when to use DMN and when SBVR, and when and how to combine the two.
DMN 1.0 contains a non-normative Annex A on the relationship between DMN and BPMN, but nothing of the kind for SBVR. The paper by Mark H. Linehan and Christian de Sainte Marie, “The Relationship of Decision Model and Notation (DMN) to SBVR and BPMN,” Business Rules Journal, Vol. 12, No. 6 (June 2011) does offer such a discussion. This paper appeared years before DMN itself, but is highly informative, not to say prophetic (BRCommunity.com is free, but you must register and get yourself a password):
http://www.BRCommunity.com/a2011/b597.html
DMN models event-based procedure calls, SBVR is bidirectional
All the elements in the DMN structure of Figs. 2 and 3 build up to a single, top-level decision: the answer to the question whether student S is allowed to enrol for course C. Such a decision is called for whenever an enrollment request (as shown in Fig. 1) occurs. DMN’s vision is that, each time such a decision must be made, input parameters are passed to a decision engine, which is then guaranteed to produce a single output value. The output value in this case is a boolean value stating whether or not student S can enrol for course C. The focus is on the input values and the output value. The rule:
“The number of students who subscribe to a course must not exceed the subscription limit of that course.”
is thus invoked (is visible, traceable) only in the event that a student wants to subscribe to a course.
However, logically, this rule is equally of interest when a registrar (for whatever reason) attempts to bring down the subscription limit of a course that already has subscriptions. In the SBVR formalisation, the rule is connected indiscriminately to the two fact types:
student subscribes to course
course has subscription limit
so that each time any of these events threatens to occur or change, the rule is invoked (visible, traceable, evaluated). This is assuming that some SBVR tool or editing facility offers easy navigation from a fact type F to all the rules that make use of F.
Visually, this difference between DMN and SBVR is symbolised by the pointing arrows in the DRD of Fig. 2 (DMN) as opposed to the non-directional association lines in the class diagram of Fig. 5 (SBVR).
In my experience, SBVR specs are welcomed by people responsible for things like legal compliance, internal policies, work instructions and quality assurance, but not by the IT department. When you compare Figs. 4 and 5 (SBVR) to Figs. 2 and 3 (DMN), it is easy to see that this is not surprising. The DMN structure maps easily to a code snippet, software component, service, etc. that is invoked by passing the input value(s) and returns the decision as an output value. The SBVR rules, by contrast, provide absolutely no clue to the optimal way of implementing their enforcement in an IT solution. With SBVR, finding that out is work that remains to be done.
DMN is currently stronger at providing overview and completeness
Because in DMN, the multiple elements that make up a decision are clustered in a hierarchical structure and the entrypoints to decision-making can be neatly tied to process steps, it is easier to get an overview of defined functionality. I believe SBVR could ultimately afford the same level of overview, but it would have to come from superior tooling that does not seem available yet.
Unlike SBVR, DMN drives at completeness: modellers are invited to provide a closed algorithm early on, in which each conceivable set of input values will always produce exactly one decision, ie. a single output value.
SBVR is easier for domain experts to validate
Admittedly, decision tables have an intuitive side; they can offer a sense of overview. DRDs are able to give a diverse audience a quick overview of a decision algorithm.
But DMN typically features an extremely detailed breakdown of the various elements of an algorithm in boxed expressions. A structure such as Fig. 3 is impossible for domain experts to comment on without expert help or specialised training.
With SBVR, it is much easier to get validation from domain experts, because the rules in Fig. 4 are formulated as concise propositions in natural business language. There is no learning curve: a validator just needs to read the rules and definitions and say whether or not they correctly state the (as-is or to-be) business conduct. The integration between rules and definitions is ideal. To validate the rule:
“The number of students who subscribe to a course must not exceed the subscription limit of that course.”
you may want to look up what is the assumed definition for ‘subscription limit’. Because SBVR arranges rules and definitions with the help of a well-defined concept structure, it is relatively easy for SBVR tool builders to make definitions of terms available whenever they are needed.
SBVR has more natural business language
Contrasting Fig. 3 and Fig. 4, it is easy to see that DMN invites you to make up long, technical noun phrases for each intermediate step, while SBVR stays much closer to what business people actually say.
A noun phrase like Student Total Courses Subscribed Count is entirely typical of DMN. Granted, it does its job of tying together corresponding elements in related boxed expressions, but it is not what people say. It doesn’t communicate well when speaking to anybody else than DMN specialists.
Leave a reply